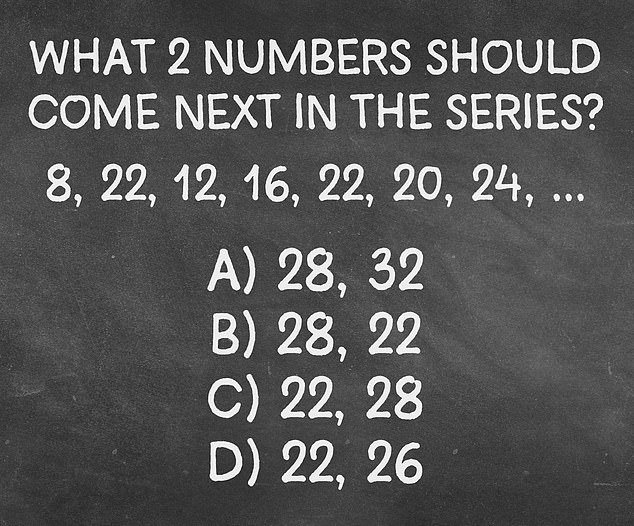La secuencia de una matemática ‘ordinaria’ sorprende a Internet, demuestra que puede ser mucho más complicada que la primera mirada.
Teaser de cerebro matemático, x usuario publicado Bholanath duttfounderSe ve una secuencia numérica preliminar con siete números.
Al principio, el orden aparentemente parece un patrón: no es tan fácilmente crujido.
La publicación se ha rascado la cabeza a Internet, los valientes participantes brindan respuestas de oposición en un intento de resolverlas.
¿Describirá el código y descubrirá los siguientes dos números de la serie? ¡Intentar!
Aquí está el pedido: 8, 22, 12, 16, 22, 20, 24, …..
A) 28, 32
B) 28, 22
C) 22, 28
D) 22, 26

Una secuencia matemática ‘ordinaria’, presentó la secuencia de un número preliminar, sorprendido de Internet, demuestra que puede ser mucho más complicado que aparecer a primera vista
La primera clave para resolver este rompecabezas alucinante es detectar un patrón, especialmente una alternativa.
¿Lo resolviste?
Si la respuesta es sí, ¡felicidades! Eres un wiz de matemáticas. Si ese no es el caso, hay una indicación aquí: el orden sigue un patrón de repetición alternativo, utilizando la adición general a la formación de su estructura, especialmente, número cuatro.
La respuesta correcta indicada por un participante es la siguiente:
8, 22, (+4), 12, 16, 22, (+4), 20, 24, 22, (+4), 28
Varios usuarios pudieron identificar con éxito la respuesta correcta, que es alternativa C: 22, 28.
El orden varía entre el patrón regular y un número ‘aleatorio’. En este caso, el número 22 aparece cada tercera vez, de repente evita el patrón regular.
Excepto 22, la secuencia se agrega a cada número agregando cuatro al patrón creando el siguiente número.

En pocas palabras, el orden confuso es seguido principalmente por una simple reglas de ‘cuatro’, pero cada tercer número se reemplaza en lugar de 22

Las conexiones entre una secuencia pueden ser más profundas sobre la propia comprensión de uno sobre los conceptos matemáticos: crear una base sólida para problemas avanzados, mejorar los problemas para resolver la eficiencia y lograr un mayor éxito en varios campos, como dinero, ciencia y tecnología.
Por ejemplo, si el número actual es 16, el siguiente será 20 (16+4).
La secuencia ‘AD 4’ rompe el número aleatorio de 22 cada tercera vez en el patrón.
Cuando el patrón generalmente agrega cuatro, 22 conjuntos se siertan a los intervalos, o cada tercera vez, interrumpe la secuencia hasta que comienza nuevamente y de lo contrario hace que la ecuación simple sea más desafiante.
En pocas palabras, la secuencia confusa es seguida principalmente por una recta reglas de ‘cuatro’, pero cada tercer número se reemplaza con 22.
Este rompecabezas es uno de los últimos de una serie que ha fascinado a los usuarios de las redes sociales en todo el mundo.
Los patrones aparecen en un elemento básico de matemáticas, números, tamaño, álgebra y la forma en que resolvemos problemas diarios.
Estos patrones pueden ayudar a predecir los eventos futuros que se reconocen, una habilidad que se puede aplicar al mundo real para predecir las tendencias.
Identificar un problema también puede reducir la complejidad de un problema, pero revela patrones y relaciones en números que no son inmediatamente obvios.
Además, todos los conceptos matemáticos vistos en una secuencia pueden profundizar la propia comprensión de todas las ideas matemáticas, creando una base sólida para problemas avanzados, mejorar los problemas para resolver la eficiencia y lograr un mayor éxito en varios campos, como dinero, ciencia y tecnología.